Part 1 of 2

Synergetics, departing from convention, replaces the cube with the regular tetrahedron as its principal unit of volume. The four-sided tetrahedron is the simplest possible enclosure — which is why mathematicians call it a “simplex”. Drawn as a cage, or wire frame, it has four windows, four corners and six edges. No space-enclosing network has fewer windows (facets) than four. The cube (or hexahedron), by contrast, has six facets, eight corners, and twelve edges, whereas a geodesic sphere may consist of hundreds or even thousands of facets!
Given the status of the simplex as “simplest space-enclosing network”, the decision to use its regular form as a unit of volume makes some sense. As a consequence of this decision, we obtain whole number volumes for other familiar shapes (including for the cube). This aesthetically pleasing and streamlining result provides additional reinforcement for those taking the time to learn this alternative (yet logical) approach to spatial geometry.
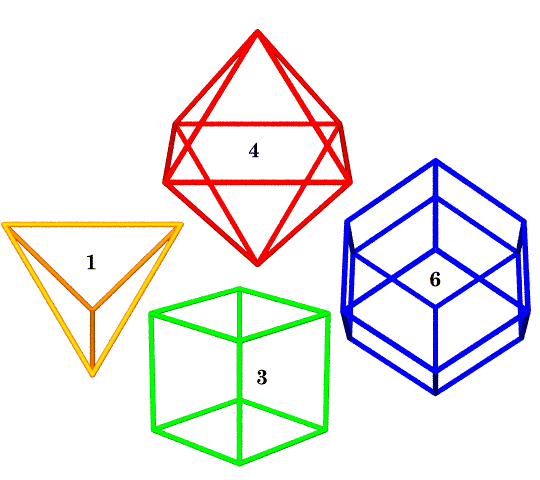
The tetrahedron has another interesting and unique property: its dual is also the tetrahedron. We get a shape’s dual by switching faces for corners and vice versa, while keeping the number of edges unchanged. The cube and octahedron are duals, as are the cuboctahedron and rhombic dodecahedron.

The dual of a shape need not be any specific size, however we may specify that the edges of the two shapes intersect at right angles. By combining duals in this way, we define the vertices of additional shapes. For example, the regular tetrahedron and its dual (also a tetrahedron) intersect to form a cube. Likewise, when we intersect the edges of a cube with its dual, the octahedron, we get the vertices of a rhombic dodecahedron.

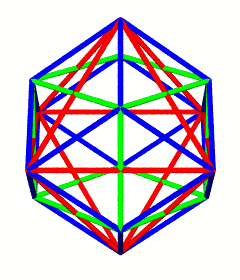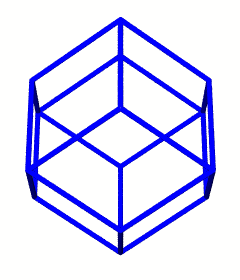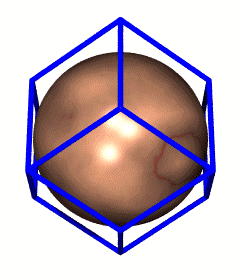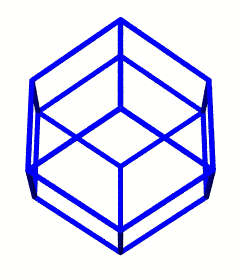
The volumes for the shapes mentioned and displayed so far are as follows:
Shape Volume Tetrahedron 1 Duo-Tet Cube 3 Octahedron 4 Rhombic Dodecahedron 6
The cube and rhombic dodecahedron are both space-fillers, meaning they fill space without gaps. The tetrahedron and octahedron fill space in complement (by working together) with twice as many tetrahedra as octahedra.
We can put spheres inside each rhombic dodecahedron of volume six, sized to touch its twelve rhombic face centers. When these volume 6 dodecahedra pack together to fill space, the spheres will be tangent to one another at these 12 “kissing points”. Each sphere will be tangent to 12 neighbors (unless at the border of the packing arrangement).

These spheres we define to be of unit radius. The unit volume tetrahedron is formed by four such spheres and has edges of 2 radii, or one diameter in length.
The 12 neighbors to each nuclear sphere in the above packing will be at the vertices of a cuboctahedron. This cuboctahedron has volume 20 relative to our sphere-diameter-edged tetrahedron of volume one. The cuboctahedron’s 12 radial (center-to-corner) and 24 circumferential (corner-to-corner) edges are all the same length: one sphere diameter (the same as the tetrahedron’s).

In Part II of The Synergetics Hierarchy of Concentric Polyhedra, the Jitterbug Transformation will be introduced as a conceptual bridge from the above family of shapes to another family with five-fold rotational symmetry.
For further reading:
- Interactive Javascript Exhibit
- LiveGraphics3D view (Java applet by Martin Kraus)
- George Hart on duals and dual-combinations
- More on the sphere packing matrix (IVM)
- An Introduction to Synergetic Crystallography
Synergetics on the Web
maintained by Kirby Urner