A Personal Account
by Kirby Urner
First Posted: Oct 3, 1997
Last Revised: Feb 9, 2010
The Oregon Math Summit, held on October 2nd, 1997, at Oregon State University in Corvallis, was certainly a valuable learning experience for me.
I took an active role, as a presenter of course, but also as the guy with the squeeky flip-chart felt pens who wrote down the points people made in the breakout session after the intro speeches by the heavy hitters. And I participated actively and constructively in Ralph Abraham’s chat session. For a grand finale, I got to run the microphone up and down and between the seats during the Q&A with Sir Roger Penrose (after first using my privileged position to get my own question in edgewise).
My Beyond Flatland presentation went OK. I packed a lot in, but it all self-reinforced, coming back to the same points from many directions. “This is starting to click” said one 5th grade teacher towards the end, after asking several good questions about the A module. Another teacher came up afterwards and mentioned having built a 3-frequency dome with his students long ago — said this material had clearly come a long way since, “lots of good geometry here” he added. A guy in front asked how long it took me to learn all this and I said about 10 years, but with all the work that’s been done to repackage synergetics in the interim, the next generation might get it down to more like 10 minutes.
My handouts contained pointers to Struck, Dome, Povray and VRML. No mention of my own site but I had that on the felt board from the end of the previous workshop in the same room, about math on the internet, wherein someone was asking about geometry websites — I was busy setting up my props for the talk and overheard the question.
I bought a new shirt, tie (computer chips motif), and green trousers for this event and stupidly left my wallet in the old pair (remembered everything but that). So come dinner I didn’t have any means and took a short nap in the front seat of the Subaru after ingesting some leftover symposium muffins. Turns out there’d been this dinner for all the invited speakers, with a name tag next to my plate and everything, but the organizers all assumed I knew about it so no one mentioned it to me (nothing in the speaker’s packet about it I don’t think). So I missed out on that one — then had to bum some bucks from Terry Bristol, ISEPP prez, to buy enough gas to make it home, that evening after the Penrose talk.
Keith Devlin showed us a video clip from a new PBS series on Mathematics making its debut in April of 1998. The show is about real people using mathematics. We saw a lot of glitzy, fast takes with a big M in each segment, finally getting to the word ‘Mathematics’ as a punch line. Ivars Peterson took this as a joke: people have this anti-math reflex so engrained in this culture that “Mathematics” is now “the M word” — we don’t dare truck it out before hooking the audience with MTV-style eye candy, or the viewers will scatter to other channels.
The consensus among the heavy hitters (each made a short presentation after drawing lots for sequence) was that computational skills and basic numeracy was something to be instilled by all teachers of all subjects (Keith was the most explicit on this), and we should recontextualize the rest, embedding “higher math” in a more humanities-style curriculum wherein students get the message that mathematics permeates every aspect of the technoculture, albiet somewhat invisibly and behind-the-scenes (given the slick interfaces) — and getting that message across is maybe more important than actually overdrilling in specific skills, which you’ll learn as you specialize, if you do, as some brand of engineer or whatever. In the meantime, we should mix in a lot of history and study mathematics through key personalities (including the teacher’s), with the basic “how to make change and read the newspaper bar graph” type skills for everyday living more diffused throughout the curriculum (Devlin again).
Of course the speakers had their differences with one another. Ralph Abraham is most into doing math in chronological order, in sync across all subjects, meaning you shouldn’t teach anything ahead of its proper time, out of sequence. His curriculum (prototyped on Long Island someplace) has first graders doing Stone Age math, up through Neolithic (emphasis on the garden — reinventing agriculture), with maybe third or fourth graders doing Babylonian clay tablet work, progressing through Egyptian, Greek, Middle Ages, Renaissance and so on up to the computer revolution in maybe eleventh grade — something like that. But Ralph is discouraged because of all the pressure to pass this or that benchmark test (e.g. the SAT), with parents crazy to have junior focus towards that goal. Plus you can’t find math teachers with all the credentials and still willing to relearn to the extent of knowing anything about Babylonian math or whatever — they come preprogrammed to teach the standard curriculum, not Ralph’s.

Personally speaking, the thought of spending my whole K-12 ontogeny slowly recapitulating math’s phylogeny sounded a bit tedious, though I’m sure high caliber teachers could make it worth my time. I’d like to have a time line on CD and the ability to access math in chrono-sequence as an option. Teachers could teach from the timeline in many lesson plans, but the whole curriculum wouldn’t be lockstep-synced to that ordering through a whole twelve year span (and beyond). Like, life’s just too short to waste a whole year pretending to be a Babylonian in my book, especially when you could be doing synergetics, which by Ralph’s standards shouldn’t be introduced until maybe the 1990s, well after we teach everything else on the time line (like in grad school or something). Actually I don’t think Ralph was considering synergetics at all as a part of his curriculum — though maybe he is a little bit since our informal meeting (I flipped through some of the dynamite transparencies I’d developed for my presentation, after establishing some credentials as a soul brother when it comes to respect for those geeky Greeks).
Sir Roger Penrose seemed into math for math’s sake more than Devlin, wanting kids to appreciate the sublime beauty of absolutely useless gizmos. But the gizmo he brought to show and tell about wasn’t all that useless. He’s been studying the Pythagorean scale of musical notes, putting the frequency ratios on a “circular slide rule” (a log scale bent around the octave), showing how you can visualize chords as angles and key changes by rotating the wheel.
But then he showed how these key changes get you these “commas” (small sinus gaps) if you go with the strictly Pythagorean frequencies, and how, ever since Bach, master of the well-behaved chord change, the piano has used an approximation (another circular transparency, this time with all pie-slices equal) wherein the ratios are all the same — it superimposes on the Pythogorean pretty well but not perfectly. Anyway, this was all useful and interesting music theory, with historical threads woven throughout. The audience was clearly entertained.

Ivars was worried about Sesame Street and MTV style fast cutting and topic hopping, noting in the breakout session that one of his kids just gets frustrated with that approach, preferring to drill down within a topic once hooked, vs. jumping from one thing to another. He’s a bit anxious about the giddy-minded approach which fast-cut TV seems to encourage.
The teachers at this event were somewhat in a tizzy about the new state standards, which get measured on a standard test. The test has just gotten a lot harder, as State Superintendent Norma Paulus reiterated in her post-lunch banquet hall speech (held in the fancy new OSU alumni center), and now most kids are likely to score rather poorly. Only half the kids in the state even take enough math in high school to have an opportunity to score well — and of those only a small percentage will actually make top marks. So the teachers are caught in a bind, getting mixed messages. The standard bearers are marshaling the rank and file to drill drill drill to score high benchmarks, while the assembled leadership from the mathematics department itself is suggesting a more Renaissance approach, with lots of team teaching and convergence of subject areas, “not trying to turn students into poor imitations of a $20 calculator” as Devlin puts it.
In the meantime, Norma Paulus (with whom Ralph was impressed) outlined her state-level coping strategy, which she’s developing in tandem with Governor Kitzhaber, to build a “firewall” around instructional time, aimed at creating an inviolate space wherein teacher-student communications might continue to develop and flourish. Plus she was encouraged by the literally truck-loads of hardware being offloaded by the corporations on the schools as they upgraded to newer equipment, which students were learning to cannibalize and reassemble into working systems. She encouraged all teachers to return to their schools and ask about all that staff development money we know is there (because of all the expense records) but which may not be getting used accountably enough from the point of view of the mathematics department.

My response, expressed in the breakout session (as the official note taker, I managed to interject twice — once about the wierdnesses in floating point math as implemented in computers, reason enough to learn the algorithms on paper as well) was that if teachers wanted to fight the standard bearers and take back control of the curriculum (they all agreed that these tests from on high were severely limiting their freedoms and creativity as teachers on the front lines) they could use the ammo I was supplying via Beyond Flatland. Here was basic, low level, primary school material that every kid should know, and yet isn’t part of the standard — clear evidence that the mathematics department knows relevant content far better than whatever officials charged with concocting these tests.
If teachers rally around obviously relevant curriculum that the standards people are oblivious about, they have a chance to convince parents that junior will get a better deal if the mathematics department is given more responsibility, not less — like I said to Ralph after his class, it’s folks like you that should be our chief curriculum designers, not committees of well-meaning bureaucrats who think they know what the curriculum should look like, and yet haven’t a clue about what Ralph Abraham is doing to enhance it.
I also emphasized “home schoolers” as a strong card in our hand, since we can always invoke this nebulous all-ages network of dedicated math students as not beholden to the state. Out here in the wilds of the web, we can experiment with whatever newfangled curricula we like, and some enlightened parents are going to clearly see that junior is getting a far better boost into a promising future from staying at home (or tuning in after hours) than by kow-towing to the text book gods and their stale recycling of whatever sold last year (octane-enhanced with whatever cosmetic improvements of course).

Alexander Graham Bell’s octet truss
Bob Burton, The OSU math prof facilitating the break-out session asked me for a specific example of what the standard curriculum is leaving out (he wondered if our math head speakers were more a “last gasp of the Renaissance?” — something I squeak-wrote on the flip-chart as a good leading question), at which point I inserted a plug for my afternoon session. “Come to Beyond Flatland and I’ll give you all the ammo you need” I announced — earlier I suggested we all use the internet to better organize and stay in touch between summits, after hours if necessary (lots of nods).
I started my talk off with ClockTet by Richard Hawkins (in association with myself), a four minute computer animation with the clock face as a central metaphor.
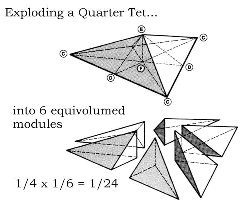
I told the class I’d show it again at the end, and they could measure their increased appreciation for its content by the new insights they’d have on second viewing — “an easy kind of test”. Then I got my 31 slides-on-tape rolling, 18 seconds per shot, running through three topics: Concentric Hierarchy, Sphere Packing and Frequency. I emphasized that most of this material was in the public domain, on the internet, and if their school had invested in a digital camera, they could duplicate my process for creating such slide shows (the handout gave more details). Then I went to the overheads and went over these same topics in more detail, every so often picking up a physical model (before class, as people were taking their seats, I passed a bunch of models around, including Russell’s high tech tensegrity coupler, plus some museum gift shop stuff) and going over the basic principles.
A couple of teachers were especially interested in the large styrofoam ball with toothpicks, green and red pipe cleaners, and black ribbon. The red pipe cleaners connect toothpick-vertices in an octahedron (volume 4), while the green make a cube (volume 3), and black ribbon outlines the 12 rhombic faces of the space-filling, sphere-containing dodecahedron (volume 6). They saw this as something they could replicate in class. I explained my process of looping rubber bands as three equators to give the XYZ framework for the octahedron — jabbing in toothpicks at the intersections and removing the rubber bands and adding red pipe cleaners. Then I basically eyeballed the octa-face centers for the cube toothpicks, and added the green pipe cleaners, topping the whole thing off with the black ribbon wrap.
I also went over Karl’s ingenious system of bent pipe cleaner joins for stuffing into thin cocktail straw edges — Russ had built several of those during his visit, sitting next to me at Megan’s Run, an annual 24 hour marathon wherein my friend Mike Hagmeier was a participant (I lap counted for four hours at Lincoln High while Russell amused himself with pipe cleaners — I later learned Mike ran 78 miles before collapsing at 3 AM). But I digress.
Ralph was just back from writing a text book in Italy — calculus with an eye towards laying the foundations of chaos theory (whatever that is, he seems deliberately fuzzy on that score). He hyped the European math curriculum quite a bit — was on sabbatical in France at some point years ago and helped his kids with their homework (in French of course). The Europeans never seemed to lose the visual link with Euclid — less cost-cutting in the graphics department, unlike in USA text books, wherein pictorial math is given short shrift. Ralph has recently put all of Euclid’s stuff on the web in the form of “dynapics” — Adobe Illustrator type GIFs taking you through all the constructions and proofs very explicitly. He’s very turned on by the Euclidean stuff — wondered if any of us knew how to construct a pentagon (takes 56 steps in Euclid Ralph told us). I said I thought I could, using two circles (I was thinking of a somewhat racist theosophy book I’d been recently perusing, L. Gordon Plummer’s The Mathematics of the Cosmic Mind Fig. 4 pg. 15 — that’s why I asked if Euclid’s solution involved constructing a decagon first).
![]()
Ralph told the teachers that more conservative minds, some of whom he much respected, had originally tried too hard to control chaos, like through the Office of Naval Research, narrowing its band of operations to something minimal and controllable. He offered this as an analogy as to what might be going on in Oregon around standards testing — too much rigidity in the face of inherently dynamical systems. Then he launched into a brief explication of what dynamical systems theory is all about (strong links to the calculus), getting around to his teaching in chronological sequence ideas.
I asked if maybe the chronological approach meant we should do more to present mathematics as a discontinuous zig zaggy evolution, with lots of dead ends and withering branches — more like the Kuhnian analysis of science’s checkered past, with all those upsetting paradigm shifts and oldsters going down with their ships and so on (that metaphor comes to me now — didn’t use it then, but did mention Kuhn). And wouldn’t this involve studying “the heresies” — like I’d just been reading Bishop Berkeley’s problems with ‘1/infinity’ as used to prove stuff in the calculus — people said they’d addressed his concerns after he died, but I thought he’d still be objecting today. “Mathematicians could sometimes be really mean dudes” I went on (thinking of those brutal dueling episodes, although the two such episodes I recall were with non-mathematicians) and math involves a lot of arguing, polemics, games with funding (like look what Kronecker did to Weierstrass and Cantor) — shouldn’t we share this with kids, instead of presenting the subject as a cold “everyone agrees” type thing? Ralph heartily agreed (he knows first hand what it means to wage an up-hill battle).
I also mentioned I thought the chaos people had a PR problem, in that the general public immediately thinks of fractals and recursive self-similarity, but Ralph hadn’t mentioned those at all. He agreed, and traced the problem to Gleick’s book, which went heavily for fractals because of all the pretty pictures. He didn’t begrudge James Gleick his million-dollar success with that book Chaos, acknowledging a narrow overlap of chaos theory with fractals in the region of strange attractors, but felt the general public had somewhat the wrong idea as a result (like, so what else is new when it comes to the general public, right?).
The evening Penrose talk was open to the general public (for a fee) with front rows roped off for us teachers and presenters. I got there early and bummed some bucks from Terry when he came in with Sir Roger, so I could get some gas for the Subaru (and a Big Mac as it turned out). Maggie Niess, OSU science-math ed chairperson and conference organizer (along with her secretary Rose) said she was sorry about the dinner snafu (I shrugged it off). Ralph took a front row seat across the aisle from me and we settled in to listen to Penrose do his thing.
 Sir Penrose has added the “tribar” as something for which he and his father should be remembered. That’s that “impossible triangle” used in those famous Escher lithographs as a basis of the forever ascending staircase and descending waterfall. The toilet paper royalties infringement was also mentioned by OSU President Paul Risser as a part of his introduction, plus we all applauded state education head Norma Paulus for making the Math Summit a reality — thanks in part to Terry’s connections (my wife Dawn is the ISEPP bookkeeper, and she was quick to suggest I would be a relevant presenter at this event, and Terry immediately agreed — really quick thinking on her part).
Sir Penrose has added the “tribar” as something for which he and his father should be remembered. That’s that “impossible triangle” used in those famous Escher lithographs as a basis of the forever ascending staircase and descending waterfall. The toilet paper royalties infringement was also mentioned by OSU President Paul Risser as a part of his introduction, plus we all applauded state education head Norma Paulus for making the Math Summit a reality — thanks in part to Terry’s connections (my wife Dawn is the ISEPP bookkeeper, and she was quick to suggest I would be a relevant presenter at this event, and Terry immediately agreed — really quick thinking on her part).
Penrose is looking for physical phenomena of a sufficiently noncomputable nature to serve as an anchor for our mental world, wherein we have access to the Platonic realm (via mathematics especially). He emphasizes that computers don’t have access to the Platonic realm, because they simply follow rules whereas although humans accept rules, and recognize new truths as consistent with them, they then proceed to transcend them by accessing truths the rules simply don’t predict or anticipate. I was thinking of Kant’s “synthetic a priori judgements” and Stuart Kaufmann’s synergetic “exaptations” as relevant in this connection.
To prove how computers can be trapped into revealing their innate stupidity by their own rule-following limitations, he had some chess problems which show at a glance how white can force a draw, but which computers, including Deep Thought and Deep Blue, all bungle, by taking the rook as bait, breaking the wall of pawns that is clearly the white king’s only defense. He went on to discuss other brilliant insights that mathematicians have had (proof of their transcendent access to the Platonic realm) which leave computers in the dust, as far as manifesting any creative intelligence is concerned.
So where in the brain do we localize the phenomena which make humans so special vis-a-vis their robot analogues? The title of the talk was The Large, The Small and the Human Mind — also the title of the upcoming book. The idea here is that we have fairly clear and deterministic models of the very large and the very small, but they don’t converge in mediophase very successfully, suggesting some new physics is needed, which will incorporate the human mind as a bridging phenomenon. The new physics will replace the conventional view that quantum mechanics goes to probabilities in mediophase, suggesting instead that it goes to certainties in short time frames with quantum gravity perhaps explaining what forces the wave function to collapse, leaving the cat dead or alive, not in some superpositional quasi-state.
Penrose is focusing on microtubes in the neurons as possibly sensitively constructed enough to register superpositions of quantum states for very short time periods, thereby allowing human consciousness make use of quantum entanglements to escape any rigid determinism and to make these leaps to higher Platonic levels even while still remaining brain-embedded in the physical world — as are the stupid computers. The difference between brains and computers is that brains are sensitive enough to register the effects of quantum gravity (whatever “gravity” is — and whatever “awareness” is, a key term Penrose was reluctant to define, but which he suggested we all know from experience).
Although he mentioned philosophy as feeding into this talk in places, Penrose made it clear that mathematics and physics were his focus areas. My question was clearly coming out of the philosophy department however — at the end I quoted Wittgenstein saying something like “if ‘consciousness’ has any meaning, it must be a humble one, like ‘table’ ‘lamp’ or ‘chair’.” I said I understood from his presentation of Gödel that we could keep enlarging the sphere of truth, consistently with accepted rules (i.e. without breaking any) but in ways not predicted by them either (thinking of Kaufmann again, though I didn’t try to stuff his “exaptations” into my question). Now that physics was feeling ambitious enough to absorb “consciouness” as another one of its key terms, I wondered if maybe the evolving usage patterns were changing its meaning, such that “consciousness” out the other end of the Penrose syllabus had a different “spin” than it had going in — a sort of moving target in other words, “a kind of zero.”
Penrose didn’t agree of course, as he sees consciousness as an objective, static thing which we all experience through qualia and experiences of emotion and understanding and so on — a view shared by the general public by and large. The goal is to discover its physical basis while consciousness itself “holds still” as we solve the surrounding puzzles. By analogy I suggested that if Newton returned he’d need some considerable reschooling to catch up on what we mean by “gravity” in this day and age (e.g. all that “shape of spacetime” stuff) and again Penrose disagreed, seeing “gravity” as a fixed point of reference as familiarly Newton’s today as ever. Obviously my view that key terms have wordmeaning trajectories within fields created from usage patterns, and do not map to reality as representational so much as operate within it as codefinitional, is not one with which Penrose feels comfortable.
I introduced my question by saying I would then follow Terry’s suggestion and run the cordless mike to others in the audience wishing to ask questions, and this I proceeded to do, although some had such booming voices I judged no amplification necessary. Audience questions focused on whether our orderly and comprehending awareness were really evidence of access to a Platonic realm or more a reflection of physical principles embedded in the design of nature, and hence the brain. Perhaps our intelligence is of local views only, with a greater universe not penetrating our thick skulls, because of no survival value (this from an Asian gentleman with a thick accent — Penrose seemed to have a hard time with it).
Towards the end of the Q&A Penrose willingly superimposed his three worlds (physical, mental and Platonic), apparently acknowledging that the mysteries associated with their interrelationships were perhaps collapsible into a single mystery of being.
People seemed honestly intrigued and engaged by the talk, although of course a lot of it went right over our heads (Ralph seemed to be nodding off in a few places I noticed, but laughed at the cartoon Penrose projected, which showed how nature probably doesn’t select for pure mathematicians, the early human kneeling in the dust with his gizmos, oblivious to his surroundings, being almost certain tiger-bait, compared to his compatriots busy doing more “useful and meaningful” applied technology type things).
I bought some gas (Arco) for the Subaru and and a Big Mac (Mickey D’s) for me and headed north to Portland on 99W, arriving home after midnight, and falling into my dreamworld while reading Feynman’s introduction to QED.
For further reading:
- Sample course outline (similar to the one included in the Beyond Flatland handout)
- Beyond Flatland: Geometry for the 21st Century (web essay)
- Mathematical Association of America home page
- The 1995 GENI Conference, another personal account
Synergetics on the Web
maintained by Kirby Urner