A Study in Sphere Packing
by Kirby Urner
First posted: October 29, 1997
Last updated: October 29, 1997
We learned in An Introduction to
Quadrays that the six edges of the quadrays' framing
tetrahedron, doubled to give positive and negative directionality,
comprise the 12 directions from the center of a cuboctahedron to
its 12 vertices.
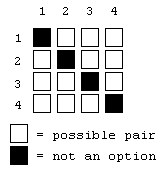
Put another way, the back and forth movements along the six edges of a regular tetrahedron provide the 12 stepwise jumps available between neighboring unit-radius sphere centers in the isotropic vector matrix. Packing outwardly in layers from a nuclear sphere, this packing takes on a cuboctahedral conformation.
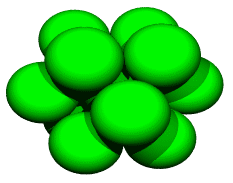
The goal of this paper is to leverage our investment in quadrays to
get some renderings of cuboctahedral sphere packings at different
frequencies. Our investment so far consists of some computer source code defining a 4D
turtle class. The turtle moves around in space in response to
either quadray or xyz inputs.
The 12 directions from a nuclear sphere center to the centers of the 12 spheres packed around it are defined by the following quadray coordinates:
(0,1,1,2) (0,1,2,1) (0,2,1,1)
(1,0,1,2) (1,0,2,1) (1,1,0,2)
(1,1,2,0) (1,2,0,1) (1,2,1,0)
(2,0,1,1) (2,1,0,1) (2,1,1,0)
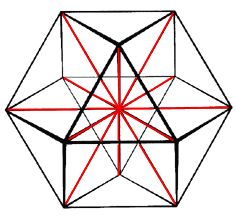
Notice that specifying the position of the 2 and the 0 unambiguously identifies these 12 quadrays, the remaining coordinates being both 1. If we say the 2nd coordinate is 2, and the 4th is 0, then we know (1,2,1,0) is the quadray meant.
With four positions (or slots) for our tokens, 2 and
0, we have 12 possibilities. The matrix at right shows all possible
position pairs, but since our tokens never share the same position,
the position pairs (1,1) (2,2) (3,3) and (4,4) are out of bounds.
That leaves 12 possibilities -- all remaining pairs once the four
along the diagonal are removed.
Note that if both tokens were the same number, like 1 and 1, we would have only six unique possibilities. The diagonal would drop out as before, plus those above the diagonal are merely position pairs with the tokens reversed -- and in the case where both tokens are the same, these mirror pairs would be identical.