![]()
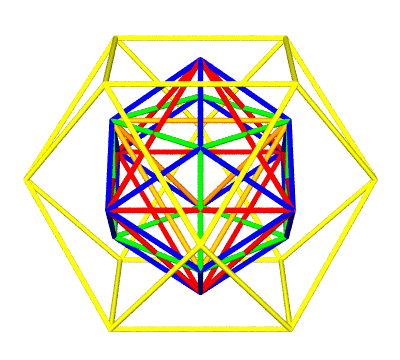
The Synergetics Hierarchy
|
![]()

|
Missing from this assembly are two of the five Platonics, the icosahedron and its dual, the pentagonal dodecahedron. What both of these missing Platonics have in common is five-fold rotational symmetry. A shape has five-fold rotational symmetry if it can be rotated around some axis by one fifth of a full circle (72 degrees) and still look exactly the same. The cuboctahedron will morph into the icosahedron by way of a transformation named "the Jitterbug" in synergetics (the jitterbug was a popular dance). To obtain the icosahedron, we add new edges to the cuboctahedron's six square faces (24 + 6 = 30 edges total), which faces distort and crease into two triangular faces apiece, for a total of 20 triangular faces. The number of corners remains the same (12) plus we keep the cuboctahedron's eight triangular faces intact (although their relative orientation changes). The resulting icosahedron has a volume of approximately 18.51, smaller than the cuboctahedron's. |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
With the icosahedron comes its dual, the pentagonal dodecahedron. The two structurally combine to form the rhombic triacontahedron. Given this proliferation of shapes, we have some aesthetic latitude when it comes to deciding how best to slip them in to our hierarchy. Of course any of these shapes may be rescaled at will. But if we think of the concentric hierarchy as a sort of storage device in memory, at makes some difference how we size things. For example, Fuller decided to "shrink wrap" his rhombic triacontahedron around the unit radius sphere, after the example of the volume six rhombic dodecahedron. He found this shrink-wrapped volume differed from precisely five by a relatively tiny amount. This seemed an intriguing enough math fact to merit further exploration, and synergetics actually ends up with two versions of the rhombic triacontahedron in its hierarchy: one with a diameter equal to the unit-radius sphere's (filled by 120 E-modules), and one scaled down by a factor of approximately 0.9995, and with a volume of precisely five (filled by 120 T-modules). |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Likewise, we have some latitude as to how we want to display the pentagonal dodecahedron amidst these other shapes. Fuller did not seem to have much interest in specifying a convention, perhaps because he came to his studies of the five-fold shapes rather late in his studies (the rhombic triacontahedron makes its first appearance in Synergetics 2). One of the classic ways to make a bridge between four- and five-fold symmetric shapes is by inscribing a cube inside the pentagonal dodecahedron such that the cube's edges diagonalize the dodecahedron's pentagonal faces. Scaling down the pentagonal dodecahedron (the icosahedron's structural dual) by a factor of 1/Root(2) brings it into this bridging relationship with the cube of volume three. |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Another relationship important to geometers places eight of the
icosahedron's 20 faces flush with the octahedron's. A scale factor
of |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
The jitterbug transformation properly orients the icosahedron and pentagonal dodecahedron for matching up with the cube and octahedron as per the above demonstrations. The shapes need only be resized, not rotated. Note that when we resize a shape, the volume changes as a 3rd powering of the scale factor. For example, if we double the edges, volume increases 8-fold, whereas halving the edges reduces volume by a factor of one eighth (1/2 x 1/2 x 1/2). In other words, the "home base" volumes may be written as coefficients in front of whatever scale factors to the 3rd power. In synergetics, the letter F (for frequency) typically represents the scale factor. If Vc = volume of the concentric hierarchy shape, and VF = volume of the resized shape, then VF = Vc x F3. Below is an enhanced volumes table. Unlike the 3,4-fold rotationally symmetrical members of the concentric hierarchy, which are whole number volumed (and fillable using A- and B-modules of volume 1/24), most of these five-fold members have relatively incommensurable (irrational) volumes (the exception being the rhombic triacontahedron of volume 5, but then its radius is incommensurable). Rounded decimals are flagged with an approximation symbol (~). The algebraic expressions behind these values may be read off component module plane nets ( see example), or derived via symbolic manipulation.
For further reading:
Synergetics on the Web |
|||||||||||||||||||||||||||||||||||||||||||||